Dando continuidade ao desenvolvimento da nossa pesquisa e ainda desenvolvendo as premissas básicas que vão reger o nosso estudo, nos reunimos e definimos o modelo NSI- Sistema Presa-predador como nossa referência de método de modelagem causal.
A história da modelagem NSI começa com Alfred Lotka (1880-1949) e Vito Volterra (1860-1940) que propuseram em 1925 e 1926, respectivamente e individualmente, um modelo para a interação entre espécies. O modelo de equações diferenciais do matemático Vito Volterra pretendia descrever o observado aumento da população de uma espécie de peixe predador, e consequente diminuição da população uma espécie de peixe presa, no Mar Adriático durante a Primeira Guerra Mundial (VOLTERRA, 1926). Simultaneamente, o químico e matemático Alfred Lotka desenvolveu um modelo para descrever reações químicas, nas quais as concentrações dos elementos químicos oscilavam, um processo semelhante àquele que ocorre com populações em competição.
Estes modelos, posteriormente denominados modelos de Lotka-Volterra, serviram de base para os modelos matemáticos posteriores utilizados para descrever a dinâmica de sistemas do tipo predador-presa. Atualmente, modelos do tipo predador-presa são usados em várias áreas do conhecimento, tais como em ciências biológicas e agrárias no controle biológico de pragas; em ciências econômicas para descrever as flutuações/oscilações em bolsas de valores e no estudo de competições de mercados; em ciências ambientais para descrever, por exemplo, a captura e emissão de carbono; entre outras aplicações. A utilização desses modelos permite uma avaliação qualitativa e quantitativa do impacto da competição em diferentes populações sejam elas populações de átomos ou moléculas, neurônios, bactérias, pragas ou indivíduos infectados ou grupos econômicos. Em consequência dessa modelagem matemática, somos levados às equações de Lotka-Volterra:
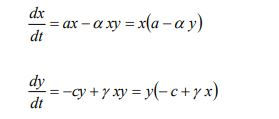
Onde
· y é o número de indivíduos de algum predador;
· x é o número da indivíduos da sua presa;
· t representa o tempo e
· α, a, γ e c são parâmetros (positivos) representando a interação entre as duas espécies.
Depois de definido o melhor modelo matemático, também escolhemos um grupo que pudéssemos trabalhar os dados e que tivesse relevância na educação da comunidade local. O Curso Assistencial Theodomiro Santigo foi a melhor opção, já que se trata de um curso pré-vestibular fundado em 2003 voltado para pessoas que não possuem condições financeiras de custear um curso preparatório particular. Conhecido pela sigla CATS, o cursinho é formado em sua grande maioria por alunos da UNIFEI, que trabalham em diversas áreas, desde a docência até a administração. Anualmente são ofertadas 100 vagas para pessoas da cidade de Itajubá e da região. Já entramos em contato com alguns responsáveis pelo curso que prontamente se disponibilizaram a nos ajudar na próxima etapa do nosso desenvolvimento, que consiste na coleta de dados.
Nosso grupo espera que de alguma forma nossa pesquisa possa impactar positivamente no trabalho maravilhoso que é realizado pelo CATS!
Referências: MODELAGEM MATEMÁTICA E ESTABILIDADE DE SISTEMAS PREDADOR-PRESA. link: https://arxiv.org/ftp/arxiv/papers/1504/1504.06244.pdf
DINÂMICA DE UM SISTEMA PRESA-PREDADOR COM PREDADOR INFECTADO POR UMA DOENÇA. link: http://w3.ufsm.br/ppgmat/images/dissertacoes/2013/SimoneOssani.pdf
Comments